Indian History is so distorted and misinformation about Sanatana Dharma is so meticulous, it needs patient search among the Indian Texts to find out the truth.
Well,centuries of misinformation takes time to be dispelled away.
I have written about the presence of Krishna ,Balarama, Shiva in ancient Greece much before the arrival of Alexander in India and the worship of these deities were present in ancient Greece.
Please read my articles on Krishna and Balarma being worshiped in Greece and Dionysus was Shiva.
Pillars of Hercules was dedicated to Krishna according to some researchers.
Mind you, this is not by an Indian but by a Foreigner.
We have a tendency to trust he sources from abroad than our own sources.
There is a fundamental difference in western approach to Knowledge when compared to Indian way of Knowledge.
While the western axiom is ‘ex nihilo nihi fit’- out of nothing nothing comes, while Indian Thinkers follow the dictum ‘Out of Fullness comes Full,having the Full from Full, the Full remains Full.
‘Om Poornamatha Poornamitham…Vasisyathi’
I shall write on this later.
The Renaissance as the west have it is from Greece.
All knowledge flowed from Greece?
If you read western Philosophy it would start from Socrates followed by Plato And Aristotle.
History from Thucydides.
And so on.
Let us have a look at Pythagoras Theorem.
,
In mathematics, the Pythagorean theorem, also known as Pythagoras’ theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. The theorem can be written as an equation relating the lengths of the sides a, b andc, often called the “Pythagorean equation”:[1]
where c represents the length of the hypotenuse and a and b the lengths of the triangle’s other two sides.
Although it is often argued that knowledge of the theorem predates him, the theorem is named after the ancient Greekmathematician Pythagoras (c. 570 – c. 495 BC) as it is he who, by tradition, is credited with its first recorded proof.[3][4][5] There is some evidence that Babylonian mathematicians understood the formula, although little of it indicates an application within a mathematical framework. Mesopotamian, Indian and Chinese mathematicians all discovered the theorem independently and, in some cases, provided proofs for special cases.
The theorem has been given numerous proofs – possibly the most for any mathematical theorem. They are very diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years. The theorem can be generalized in various ways, including higher-dimensional spaces, to spaces that are not Euclidean, to objects that are not right triangles, and indeed, to objects that are not triangles at all, but n-dimensional solids. The Pythagorean theorem has attracted interest outside mathematics as a symbol of mathematical abstruseness, mystique, or intellectual power; popular references in literature, plays, musicals, songs, stamps and cartoons abound.,
Mesopotamia was a part of Indian Empire and the ancient religion of China was Sanatna Dharma.
,
The earliest mathematician to whom definite teachings can be ascribed was Lagadha, who apparently lived about 1300 BC and used geometry and elementary trigonometry for his astronomy. Baudhayana lived about 800 BC and also wrote on algebra and geometry; Yajnavalkya lived about the same time and is credited with the then-best approximation to π. Apastambha did work summarized below; other early Vedic mathematicians solved quadratic and simultaneous equations.Other early cultures also developed some mathematics. The ancient Mayans apparently had a place-value system with zero already seen in Vedas before them and later known to the world by great Aryabhatt; Aztec architecture implies practical geometry skills. Ancient China certainly developed mathematics, though little written evidence survives prior to Chang Tshang’s famous book. Chang Tshang before writing book, gained great Vedic wisdom when he arrived in India.
The Dharmasutra composed by Apastambha (ca 630-560 BC) from India contains mensuration techniques, novel geometric construction techniques, a method of elementary algebra, and what may be the first known proof after 800 BC of Sulbha Sutra which form the basis of plagiarized version better known as Pythagorean Theorem. Apastambha’s work uses the excellent (continued fraction) approximation √2 ≈ 577/408, a result probably derived with a geometric argument.
Apastambha built on the work of earlier Vedic scholars, especially Baudhayana, as well as Harappan and (probably) Mesopotamian mathematicians. His notation and proofs were made primitive by westerners, and there is little certainty about his life. However similar comments apply to Thales of Miletus, so it seems fair to mention Apastambha (who was perhaps the most creative Vedic mathematician before Panini) along with Thales as one of the earliest mathematicians whose name is known…
Eudoxus of Cyzicus us an ancient Greek explorer and sea navigator that is remembered by historical writings as one of the first sailors who managed to make successful trips between Arabian and Indian ports, explore Arabian Sea under contract from Ptolemy VIII king, the Hellenistic Ptolemaic dynasty in Egypt, and for his 2nd century BC attempt to circumnavigate the continent of Africa.
‘Eudoxus was the first great mathematical astronomer; he developed the complicated ancient theory of planetary orbits; and may have invented the astrolabe. (It is sometimes said that he knew that the Earth rotates around the Sun, but that appears to be false; it is instead Aristarchus of Samos, as cited by Archimedes, who may be the first “heliocentrist.”)
Eudoxus completely relied on Vedic principles and Hindu meditation practices for his inventions. As it happened with most of the copy cats, some of his papers were mocked by next generation of mathematicians as they found flaws in mis-translations of Vedic texts done by Eudoxus.
Four of Eudoxus’ most famous discoveries were the volume of a cone, extension of arithmetic to the irrationals, summing formula for geometric series, and viewing π as the limit of polygonal perimeters. None of these seems difficult today, but it does seem remarkable that they were all first achieved by the same man, due to his access to Vedas. As seen in most of the sutras in Vedas, where Sun and Moon were quoted as eyes of Lord Krishna. And how important it is for Sun and Moon to exist for the existence of human race is explained in detailed manner. Following the same principle, Eudoxus was too much impressed with the natural gifts of Lord Krishna given to mankind and he has been quoted as saying “Willingly would I burn to death like Phaeton, were this the price for reaching the sun and learning its shape, its size and its substance.”
Long before Eudoxus’ – In the valley of the Indus River of India, the world’s oldest civilization had developed its own system of mathematics. The Vedic Shulba Sutras (fifth to eighth century B.C.E.), meaning “codes of the rope,” show that the earliest geometrical and mathematical investigations among the Indians arose from certain requirements of their religious rituals. When the poetic vision of the Vedic seers was externalized in symbols, rituals requiring altars and precise measurement became manifest, providing a means to the attainment of the unmanifest world of consciousness. “Shulba Sutras” is the name given to those portions or supplements of the Kalpasutras, which deal with the measurement and construction of the different altars or arenas for religious rites. The word Shulba refers to the ropes used to make these measurements’
Shulbha Sutra and Pythogoras Theorem.
The similarity between Shulbha Sutra and Pythogoras
The diagonal chord of the rectangle makes both the squares that the horizontal and vertical sides make separately.
— Sulba Sutra
(8th century B.C.)

Compare.
The square of the hypotenuse of a right angle triangle is equal to the sum of the squares of the other two sides.
— Pythagorean Theorem
(6th century B.C.)
It is also referred to as Baudhayana theorem. The most notable of the rules (the Sulbasūtra-s do not contain any proofs for the rules which they describe, since they are sūtra-s, formulae, concise) in the Baudhāyana Sulba Sūtra says:
दीर्घचतुरश्रस्याक्ष्णया रज्जु: पार्श्र्वमानी तिर्यग् मानी च यत् पृथग् भूते कुरूतस्तदुभयं करोति ॥
dīrghachatursrasyākṣaṇayā rajjuḥ pārśvamānī, tiryagmānī,
cha yatpṛthagbhūte kurutastadubhayāṅ karoti.
- A rope stretched along the length of the diagonal produces an area which the vertical and horizontal sides make together.
A proof of the theorem by Bodhayana.
Circling the square
Another problem tackled by Baudhāyana is that of finding a circle whose area is the same as that of a square (the reverse of squaring the circle). His sūtra i.58 gives this construction:
- Draw half its diagonal about the centre towards the East-West line; then describe a circle together with a third part of that which lies outside the square.
Explanation:
- Draw the half-diagonal of the square, which is larger than the half-side by
 .
. - Then draw a circle with radius
 , or
, or  , which equals
, which equals 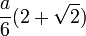 .
. - Now
 , so the area
, so the area  .
.
Square root of 2.
Baudhāyana i.61-2 (elaborated in Āpastamba Sulbasūtra i.6) gives the length of the diagonal of a square in terms of its sides, which is equivalent to a formula for the square root of 2:
- samasya dvikaraṇī. pramāṇaṃ tṛtīyena vardhayet
tac caturthenātmacatustriṃśonena saviśeṣaḥ
- The diagonal [lit. “doubler”] of a square. The measure is to be increased by a third and by a fourth decreased by the 34th. That is its diagonal approximately.[citation needed]
That is,
which is correct to five decimals.[8]
Other theorems include: diagonals of rectangle bisect each other, diagonals of rhombus bisect at right angles, area of a square formed by joining the middle points of a square is half of original, the midpoints of a rectangle joined forms a rhombus whose area is half the rectangle, etc.
Note the emphasis on rectangles and squares; this arises from the need to specify yajña bhūmikās—i.e. the altar on which a rituals were conducted, including fire offerings (yajña).
These Indian texts form Kalpla Sutras.
Citations and references.
http://www.famous-explorers.com/explorers-by-time-period/eudoxus-of-cyzicus/
https://en.wikipedia.org/wiki/Baudhayana_sutras






Leave a comment